https://w.soundcloud.com/player/?visual=true&url=https%3A%2F%2Fapi.soundcloud.com%2Ftracks%2F1678197858&show_artwork=true&maxheight=1000&maxwidth=1100

Տիտանը (քիմիական նշան – Ti, լատիներեն Titanium) 4-րդ խմբի քիմիական տարր է (ըստ հնացած դասակարգման՝ չորրորդ խմբի երկրորդական ենթախումբ՝ IVB), Դ. Ի. Մենդելեևի քիմիական տարրերի պարբերական աղյուսակի չորրորդ շրջանը։ 22 ատոմային համարով։ Վերաբերում է անցումային մետաղներին։ Տիտանի պարզ նյութը նորմալ պայմաններում արծաթափայլ սպիտակ գույնով բաց մետաղ է։ Ունի բարձր կոռոզիոն դիմադրություն:

Պատմությունը

Տիտանի երկօքսիդի (TiO2) հայտնաբերումը կատարվել է գրեթե միաժամանակ և միմյանցից անկախ անգլիացի Վ. Գրեգորի և գերմանացի քիմիկոս Մ. Գ. Կլապրոտի կողմից։ Վ. Գրեգորը, ուսումնասիրելով մագնիսական գունավոր ավազի բաղադրությունը (Կրիդ, Կորնուոլ, Անգլիա, 1791), մեկուսացրեց անհայտ մետաղի նոր «հող» (օքսիդ), որը նա անվանեց մենակեն։ 1795 թվականին գերմանացի քիմիկոս Կլապրոտը հայտնաբերեց նոր տարր հանքային ռուտիլում և այն անվանեց տիտան: Երկու տարի անց Կլապրոտը հաստատեց, որ ռուտիլը և մենակեն հողը նույն տարրի օքսիդներն են, ինչից էլ առաջացել է Կլապրոտի առաջարկած «տիտան» անվանումը։ Տասը տարի անց տիտանի հայտնաբերումը տեղի ունեցավ երրորդ անգամ. ֆրանսիացի գիտնական Լ. Վոկելենը հայտնաբերեց տիտանը անատազում և ապացուցեց, որ ռուտիլն ու անատազը տիտանի օքսիդներ են:

Տիտանի մետաղի առաջին նմուշը ստացվել է 1825 թվականին շվեդ J. J. Berzelius-ի կողմից։ Տիտանի բարձր քիմիական ակտիվության և մաքրման դժվարության պատճառով հոլանդացի Ա. վան Արկելը և Ջ. դե Բուրը 1925 թվականին TiI4-ի տիտան յոդիդի գոլորշու ջերմային տարրալուծմամբ ստացան Ti-ի մաքուր նմուշ։

Տիտանը չգտավ արդյունաբերական կիրառություն, քանի դեռ 1940 թվականին լյուքսեմբուրգցի Վիլհելմ Կրոլը արտոնագրեց մի պարզ մագնեզիում-ջերմային մեթոդ՝ տիտանի մետաղը տետրաքլորիդից վերացնելու համար։ Այս մեթոդը (Kroll process (անգլերեն) ռուսերեն) մինչ օրս մնում է տիտանի արդյունաբերական արտադրության հիմնականներից մեկը:

Անվան ծագումը

Մետաղն իր անունը ստացել է ի պատիվ տիտանների, հին հունական դիցաբանության հերոսների, Գայայի երեխաների: Տարրի անվանումը տվել է Մարտին Կլապրոտը քիմիական նոմենկլատուրայի վերաբերյալ իր տեսակետներին համապատասխան՝ ի տարբերություն ֆրանսիական քիմիայի դպրոցի, որտեղ նրանք փորձում էին տարրն անվանել իր քիմիական հատկություններով։ Քանի որ գերմանացի հետազոտողն ինքը նշել է նոր տարրի հատկությունները միայն դրա օքսիդից որոշելու անհնարինությունը, նա դրա համար անուն ընտրեց առասպելաբանությունից՝ նախկինում հայտնաբերած ուրանի անալոգիայով:

Շրջապատից մեկուսացված մարմինը կփոխի՞ իր արագությունը,թե ոչ:

Ոչ

2.Բերել մարմինների փոխազդեցության օրինակներ

Գնդակը խփում ենք պատին, նա հարվածում է պատին և գնդակը հետ է գալիս, որովհետև գնդակը ազդում է պատի վրա, պատն էլ գնդակի վրա:

3.Մարմնի ո՞ր հատկությունն է կոչվում իներտություն

Այս և բազմապիսի այլ օրինակներ ցույց են տալիս, որ բոլոր մարմիններն օժտված են այնպիսի հատկություններով, որ նրանց արագությունն ակնթարթորեն չի կարելի փոխել և դա կոչվում է իներտություն:

4.Ո՞ր մեծությունն են անվանում մարմնի զանգված

Մարմնի իներտությունը քանակապես բնութագրում է զանգված կոչվող մեծությունը:

5.Ինչպե՞ս կարելի է չափել մարմնի զանգվածը

Չափման միավորներով

6.Ի՞նչ միավորներով է արտահայտվում զանգվածը

Զանգվածը արտահայտվում է m տառով:

7.Ի՞նչն է զանգվածի չափանմուշը, միավորների ՄՀ-ում

ա.ծանոթացում զանգվածի չափման գործիքների հետ

բ.ծանոթացում կշռման կանոններին

գ. տարբեր մարմինների զանգվածների որոշումը լծակավոր կշեռքի և կշռաքարերի միջոցով

Ծանոթանալ․ Է.Ղազարյանի դասագրքից էջ 43-ից էջ48

Գ.Մխիթարյանի <<Գիտելիքների ստուգման առաջադրանքներ մաս I>>-ից էջ26-ից մինչև էջ29-ը:

Մարմինների փոխազդեցությունը

Նպատակը

Անրաժեշտ սարքեր և նյութեր: Երկու սայլակներ, որոնցից մեկի դիմաց ամրացված է թիթեղ, թել մկրատ լուցկի.

Փորձ 1

Աշխատանքի ընթացքը.

Վերձրեցի այն սայլակը, որի դիմաց առանձգական թիթեղ է ամրացված.

Ճկեցի թիթեղը և այն կապեցի թելով, և դրեցի սեղանի վրա, այն սեղանի նկատբամբ դադարի վիճակում, այրեցի թելը.

Եզրակացություն.

Առանձնական թիթեղը ուղվեց, բայց սայլակը չշարժվեց.

Փորձ 2

Հարցեր և առաջադրանքներ։

1․ Գրել եռանկյունների հավասարության առաջին հայտանիշը։

Եթե մի եռանկյան երկու կողմերը և դրանցով կազմված անկյունը համապատասխանաբար հավասար են մյուս եռանկյան երկու կողմերին և դրանցով կազմված անկյանը, ապա այդպիսի եռանկյունները հավասար են:

2․Գրել եռանկյունների հավասարության երկրորդ հայտանիշը։

Եթե մի եռանկյան կողմն ու նրան առընթեր երկու անկյունները համապատասխանաբար հավասար են մյուս եռանկյան կողմին և նրան առընթեր երկու անկյուններին, ապա այդ եռանկյունները հավասար են:

3․ ABC և MNK եռանկուններում AB=MN, ∠BAC=∠NMK, ∠ABC=∠MNK: Հավասա՞ր են ABC և MNK եռանկունները։

Այո, այս եռանկյունները հավասար են, ըստ առաջին եռանկյան հայտանիշի։

4. ABC եռանկյունում AB=8, ∠A=40⁰, ∠B=84⁰, իսկ MNK եռանկյունում MN=8, ∠M=40⁰, ∠K=84⁰։ Տեղի ունե՞ն եռանկյունների հավասարության երկրորդ հայտանիշի պայմանները։

Եթե մի եռանկյան կողմն ու նրան առընթեր երկու անկյունները համապատասխանաբար հավասար են մյուս եռանկյան կողմին և նրան առընթեր երկու անկյուններին, ապա այդ եռանկյունները հավասար են:

Ըստ երկրորդ հայտանիշի այս եռանկյունները հավասար են, քանի որ AB=MN, իսկ մյուս երկու անկյունները նույնպես իրար հավասար են։

5․Նկարում ∠BAC=∠ACD, ∠BCA=∠CAD: Հավասա՞ր են արդյոք ABC և ADC
եռանկյունները:

AC-ն ընդհանուր կողմ է, ուրեմն եռանկյունները իրար հավասար են ըստ երկրորդ հայտանիշի։

6․AB և CD հատվածները հատվում են AB հատվածի O միջնակետում, ∠OAD=∠OBC:

ա) Ապացուցեք, որ ΔCBO = ΔDAO։

Այս եռանկյունները իրար հավասար են, քանի որ նրանք հակադիր են։ Ինչպես նաև AB կողմերը ընդհանուր են, և ըստ դրա նաև բութ անկյունները։

բ) Գտեք BC-ն և CO-ն, եթե CD=24 սմ, AD=17սմ։

Ստացված եռանկյուններն իրար հավասար են, իսկ հատվող հատվածները նույնպես։ AD=17սմ հատևաբար՝ BC=17սմ։ CD=24 սմ-ի միջնակետը O-ն է, այսինքն ՝ 24:2=12սմ։

CO=12սմ

BC=17սմ

7․Տրված է ∠1 = ∠2, ∠ 3 = ∠4:

ա) Ապացուցեք, որ ΔABC = ΔCDA:

Այս եռանկյունները իրար հակադիր են, և ըստ եռանկյան հայտանիշների իրար հավասար են։

բ)Գտեք AB-ն և BC-ն, եթե AD=19 սմ, CD=11 սմ:

AB=11 սմ

BC=19 սմ

Այս անկյունները նախ հակադիր են, հետո իրար վրա ծալելուց համընկնում են բոլոր ծայրերը։

8․Ըստ նկարի տվյալների՝ ապացուցեք, որ OP=OT, ∠P = ∠T

Այս երկու եռանկյունները իրար հակադիր են, և ծալելուց ընկնում են իրար վրա։ Եվ ըստ հավասարության երկու հայտանիշների, կողմերը և անկյունները լինելով իրար հավասար, ստացվում է հավասար եռանկյուն։

9․ Ապացուցել, որ հավասարասրուն եռանկյան հիմքին տարված միջնագիծը նաև կիսորդ է և ու բարձրություն։

Հավասարասրուն եռանկյունն ունի որոշ հատկություններ, որ ուրիշ եռանկյունները չունեն․ դրանցից մեկն էլ հենց սա է։

Հավասարասրուն եռանկյան հիմքին տարված բարձրությունը նաև կիսորդ է և միջնագիծ:

Թեմա՝ Վարժությունների լուծում

1․Արտահայտությունը գրել միանդամի տեսքով.
ա) 3ax + 5ax=8ax

բ) 25 x² − 4xx=21 x²

գ) 12a b² − 5a b²=7 a b²
դ) 3 x² − 7 x² + 13xx=9x²

ե) bbc − 12bcb + b5bc=-6bbc

զ) −14yyz + 11 y² z − 2 y² z=-1y² z

2․Միանդամը բերել կատարյալ տեսքի.
ա) -25aaabb c²=-25a³b² c²

բ) −3xxxy=-3x³y

գ) x8xy5y=40x² y²

դ) −2 a² 7b²=-14a² b²
ե) 5=5

զ) −1 a²= −a²

է) 1aab=a²b

ը) − 7/4yx=-7/4xy

3․Ներկայացրել աստիճանի տեսքով.
ա) a² ⋅ a⁵=a⁷

բ) b² ⋅ b²=b⁴

գ) 5³ ⋅ 5⁷=5^10

դ) (−2 )² ⋅ 2³=-4^5
ե) (−x )³ ⋅ (−x )⁵=x^8

զ) 2ⁿ ⋅ 4²=8ⁿ⁺²

է) 3ⁿ ⋅ 3ⁿ⁺¹=3^{n^2+1}

ը) 5^k ⋅ 5^l=5^k+l

4․Արտադրյալը գրել կատարյալ տեսքով.
ա) b² ⋅ b⁵ ⋅ b²=b^9

բ) a¹ ⋅ a² ⋅ a³ ⋅ a⁴ ⋅ a⁵=a^15
գ) xxy ⋅ yzz ⋅ zxx=x⁴ y^2 z^3

դ) 4s² ⋅ ( − 5)ts ⋅ r² t² s=-20s^4 t^3 r²

5. Բացել փակագծերը և գրել բազմանդամի կատարյալ տեսքով.
ա) a(b + c)=ab+ac

բ) 3x(x − 2)=3x²-6x

գ) 3(5x − 7)=15x^3-21

դ) 3x ²(4x − 6y + 13z)=12x^3-18x²y+39x²z

ե) 2³ x(5x ² − 11)=40x^3-88x

զ) −2c(bc + 5c²d)=-2bc^2-10c^3d

6․Հաշվել արտահայտության արժեքը.
ա) 3x ² + 5x − 2x ², երբ x = 6,

3 6 ² + 5 6 − 2 6 ²
բ) ab ² c ³d, երբ a = 2, b = 3, c = 4, d = 0,
գ) a ³ + 7a − a ² ⋅ a, երբ a = 8,
դ) 2xy + 7x ⋅ y + y ⋅ x, երբ x = 5, y = 2,
ե) (a + b)² − (a − b)², երբ a = 8, b = 2,
զ) xyz − 7³, երբ x = y = z = 7:

7․Արտադրյալը գրել կատարյալ բազմանդամի տեսքով.
ա) ax(x + 5), բ) x ²(5 − x + y), գ) a ²(a + b + 1),
դ) 3a( x ² − 5x), ե) (2x ³ − 7x) ⋅ 2a ², զ) 4x( y ² − 1),
է) a ² (−2b + 4a 2), ը) −2ax(3x − 5a), թ) x y ²( x ² y − x + 2y):

8. Բերել կատարյալ տեսքի.

ա) (3x − 1)(5x + 4) − 15x ² , բ) (2x − 3)(2x + 3) − x(5 + 4x) ,
գ) 21x ² + (1 − 3x)(2 + 7x) ,
դ) x ² + x(6 − 2x) + (x − 1)(2 − x) − 1,
ե) 3x ² − x(8 − x) + (2x − 4)(2x + 4),
զ) (3x − 2)(x + 4) — 3(x + 5)(x − 1) + 1

9․Բազմանդամը վերլուծել արտադրիչների.
ա) ax + 2by ² + a y ² + 2bx, բ) 2 − ax − x + 2a,
գ) 2ab − 5b − 6ac + 15c, դ) x ² + xz + x + ax + az + a:

10․Արտահայտությունը գրել բազմանդամի կատարյալ տեսքով.
ա) 4xxy − 5y x ² + 7x ² y − xyx,
բ) 15x ² xy + 3x ³ y ⋅ 4y 2 − x ² y ² ⋅ 9xy − 11x ³ y ³ + 8x x ² y ³,
գ) a + (b − (b − a)), դ) 5a2 − (9a2 − b2),
ե) 12ab(a² + b) − 3a² b(4a + 2b),
զ) 6a²(abb − b²) + 3a((ab)² − 2ab²)

Հարցեր և առաջադրանքներ։

1․ Ի՞նչ են անվանում ամբողջ արտահայտություն:

Ամբողջ արտահայտություն անվանում են այնպիսի հանրահաշվական արտահայտությունը, որում մի քանի բազմանդամներ միացված են գումարման, հանման և բազմապատկման նշաններով։

2․Ինչպե՞ս են հաշվում ամբողջ արտահայտության արժեքը:

Թվային արտահայտության պարզեցման արդյունքում ստացվում է թիվ, որը կոչվում է թվային արտահայտության արժեք:

3․ Ո՞ր արժեքներն են կոչվում թույլատրելի։

Եթե տառերի որոշակի արժեքների դեպքում հանրահաշվական արտահայտությունն ունի թվային արժեք, ապա փոփոխականի այդ արժեքները կոչվում են թույլատրելի:

4․Հաշվե՛ք ամբողջ արտահայտության արժեքը, եթե  x=10

ա) x-6=10-6=4

բ) x²+7=10²+7=100+7=107

5.Հաշվեք  արտահայտության արժեքը, եթե a=5, b=8

ա) a+b-6=5+8-6=7

բ) 4ab=458=160

6․Հաշվե՛ք ամբողջ արտահայտության արժեքը, եթե  x=-10

ա) 3x-8=3-10-8=-1

բ) 2x²+4x+1=2(-10)²+4(-10)+1=161

գ) x⁴+3x³+8x²+x=-10⁴+3(-10)³+8(-10)²+(-10)=10,000+(-27,000)+800+(-10)=-27,010+10,800=-16,210

7.

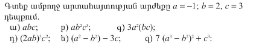
ա)-123=-6

բ)-12³3³=216

գ)3(-1)²(2×3)=18

դ)2(-1)23=-46

ե)(-1-2)-9=-12

զ)7(-1-2)+3=-18

8․

Պարզեցրե՛ք արտահայտությունը և հաշվե՛ք արժեքը փոփոխականի տվյալ արժեքի դեպքում.
ա) (7x − 3) − (4x + 1), երբ x = 2,

(72 − 3) − (42 + 1)=11-9=2
բ) (a/2 + 8) − (2a − 6) + (3a/2 + 1), երբ a = 5,

(5/2 + 8) − (25 − 6) + (35/2 + 1)=10,1-4-6=0,1
գ) y − (y + 1) + 2(y + 5), երբ y = 0,

0 − (0 + 1) + 2(0 + 5)=0
դ) (3b − 2) + (b + 1), երբ b = 2,

(32 − 2) + (2 + 1)=4+3=7
ե) x + (2x − 1) − (2 − 3x), երբ x = −1

-1 + (2-1 − 1) − (2 − 3-1)=-1