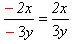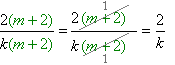Մեր շրջակայքի շատ առարկաներ ունեն այնպիսի զուգահեռանիստի տեսք, որի բոլոր նիստերը ուղղանկյուններ են: Այդպիսի առարկաներ են շենքերը, սենյակները, տուփերը, պահարանները:

Զուգահեռանիստը, որի կողմնային կողերն ուղղահայաց են հիմքին կոչվում է ուղիղ զուգահեռանիստ:

Այն ուղիղ զուգահեռանիստը, որի հիմքերն ուղղանկյուններ են կոչվում է ուղղանկյուն զուգահեռանիստ կամ պարզապես՝ ուղղանկյունանիստ:

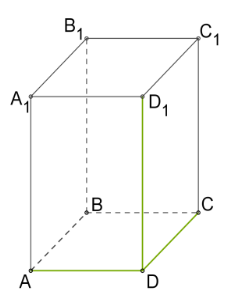
Քանի որ ցանկացած ուղիղ զուգահեռանիստի կողմնային կողերն ուղղահայաց են հիմքին, ապա ուղղանկյունանիստի կողմնային նիստերն ուղղանկյուններ են:

Ուղղանկյունանիստի բոլոր վեց նիստերը ուղղանկյուններ են:

Advertisement

Ուղղանկյունանիստի ընդհանուր գագաթով երեք կողերի երկարությունները անվանում են ուղղանկյունանիստի չափսեր՝ երկարություն, լայնություն, բարձրություն:

Այն ուղղանկյունանիստը, որի բոլոր կողերը հավասար են, կոչվում է խորանարդ:

Պարզ է, որ խորանարդի բոլոր նիստերը միմյանց հավասար քառակուսիներ են:

Ուղղանկյունանիստի բոլոր չորս անկյունագծերը հավասար են, հատվում են մի կետում և հատման կետում կիսվում են:

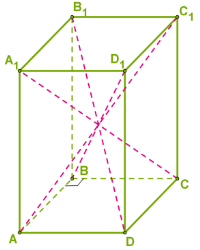
Եթե ACC₁ ուղղանկյուն եռանկյունից արտահայտենք ուղղանկյունանիստի անկյունագիծը՝ AC₁²=AC²+CC₁²,

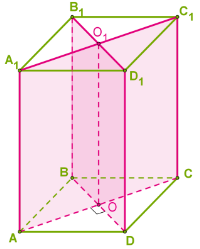
և ADC ուղղանկյուն եռանկյունից արտահայտենք հիմքի անկյունագիծը՝ AC²=AD²+DC², ապա ստանում ենք՝ AC₁²=AD²+DC²+CC₁²

Ուղղանկյունանիստի անկյունագծի քառակուսին հավասար է նրա երեք չափսերի քառակուսիների գումարին՝ D²=a²+b²+c²

Հարցեր և առաջադրանքներ։

1․ Ո՞ր մարմինն է կոչվում ուղղանկյունանիստ։ GEOGEBRA ծրագրով գծել ուղղանկյունանիստ։

Այն ուղիղ զուգահեռանիստը, որի հիմքերն ուղղանկյուններ են կոչվում է ուղղանկյուն զուգահեռանիստ կամ պարզապես՝ ուղղանկյունանիստ:

2․ Ի՞նչ երկրաչափական պատկերներից է կազմված ուղղանկյունանիստը։

Ուղղանկյունանիստը կազմված է 4 ուղղանկյունից և 2 քառակուսուց

3․ Ո՞ր մարմինն է կոչվում խորանարդը։ GEOGEBRA ծրագրով գծել խորանարդ։

Այն ուղղանկյունանիստը, որի բոլոր կողերը հավասար են, կոչվում է խորանարդ:

4․ Քանի՞ նիստ, կող, գագաթ ունեն ուղղանկյունանիստն ու խորանարդը։

Ուղղանկյունանիստ – 6 նիստ, 12 կող, 8 գագաթ
Խորանարդը – 6 նիստ, 12 կող, 8 գագաթ

5․ Որո՞նք են ուղղանկյունանիստի չափումները։

Advertisement

Ուղղանկյունանիստի երկարությունը, լայնությունը եւ բարձրությունը ունեն ընդհանուր անվանում՝ ուղղանկյունանիստի չափումներ։

6․ Համեմատել խորանարդը և ուղղանկյունանիստը։

Նման են, որովհետև եռաչափ մարմիներ են 12 կող 6 նիստ և 8 գագաթ։ Տարբերվում են նրանով, որ ուղանկյունանիստի նիստը ուղղանկյուն է, իսկ խորանարդինը քառակուսի է։

7․ Տրված է հետևյալ ուղղանկյունանիստը:

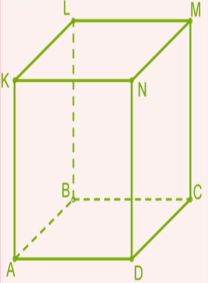
Ո՞րն է ուղղանկյունանիստի անկյունագծի հաշվման բանաձևը:  Ընտրել ճիշտ բանաձև(եր)ը:

• KM²=KN²+NM²
• AM²=AD²+DC²+CM²
• BN²=BD²+DN²

8․ Հայտնի են ուղղանկյունանիստի նույն գագաթից ելնող կողերի երկարությունները՝  10 սմ,  2 սմ  և  4 սմ: Գտնել  ուղղանկյունանիստի անկյունագծի քառակուսու երկարությունը:  

10²+2²+4²=100+4+16=120

9․ Հայտնի են ուղղանկյունանիստի հիմքի կողերի երկարությունները՝ 16 սմ, 24 սմ և  ուղղանկյունանիստի  անկյունագծի երկարության քառակուսին՝ 857: Գտնել ուղղանկյունանիստի բարձրությունը:

c²=857-16²-24²
c²=857-256-576
c²=25

10․ Որոշիր խորանարդի d անկյունագիծը, եթե նրա մի նիստի մակերեսը S=49սմ²է:

d=3a²
d=49+49+49=147սմ²
d=147սմ²

Թվային արտահայտությունը կազմվում է թվերից, թվաբանական գործողությունների նշաններից և փակագծերից:

Թվային արտահայտության գործողությունների արդյունքում ստացված թիվը կոչվում է թվային արտահայտության արժեք:

Եթե արտահայտության մեջ պատահում է բաժանում զրոյի վրա, ապա այդ արտահայտությունն արժեք (իմաստ) չունի: Զրոյի վրա բաժանել չի կարելի:  

(−3)²+5⋅0,2 թվային արտահայտության արժեքը հավասար է 10-ի:

(7−(−2)5+(6⋅4))/0 արտահայտությունն արժեք չունի:

Եթե թվային արտահայտությունը պարունակում է նաև տառեր (կամ միայն տառեր), ապա այն կոչվում է հանրահաշվական արտահայտություն:

(−3)²+5x; 3a+4b; (2x−6)/3 արտահայտությունները հանրահաշվական են:

Հանրահաշվական կոտորակ կոչվում է A/B տեսքի արտահայտությունը, որտեղ A-ն որևէ բազմանդամ է, իսկ B-ն՝ ոչ զրոյական բազմանդամ:

Հանրահաշվական կոտորակը բազմանդամի և ոչ զրոյական բազմանդամի քանորդ է:

x/(x−3); (b−1)/(b+6); (1+x³)(x²+1); (y+2)/(y²−6y+6) արտահայտությունները հանրահաշվական կոտորակներ են:

Մեկ փոփոխականով արտահայտության որոշման տիրույթ կոչվում է փոփոխականի բոլոր այն արժեքների բազմությունը, որոնց համար արտահայտությունն իմաստ (արժեք) ունի:   

Որոշման տիրույթի ցանկացած կետում արտահայտությունն ունի արժեք:  

Օրինակ` Գտնենք (x−3)/x(x+8) հանրահաշվական կոտորակի որոշման տիրույթը:

Լուծում. (x−3)/x(x+8) հանրահաշվական կոտորակը որոշված է x փոփոխականի բոլոր այն արժեքների համար, որոնց դեպքում կոտորակի x(x+8) հայտարարը հավասար չէ 0-ի: Հետևաբար որոշման տիրույթին չպատկանող x -ի արժեքները գտնելու համար պետք է լուծել հետևյալ հավասարումը՝

x(x+8)=0

Յուրաքանչյուր արտադրիչ հավասարեցնում ենք զրոյի՝

x=0 և x+8=0

x=−8

Պատասխան՝ տրված հանրահաշվական կոտորակի որոշման տիրույթը բաղկացած է բոլոր իրական թվերից, բացի 0 և −8 թվերից:

Հանրահաշվական կոտորակի որոշման տիրույթը բաղկացած է բոլոր այն իրական թվերից, որոնց դեպքում կոտորակի հայտարարը հավասար չէ 0-ի:

Հանրահաշվական կոտորակների հիմնական հատկությունը

Հանրահաշվական կոտորակի արժեքը չի փոխվի, եթե նրա համարիչը և հայտարարը բազմապատկենք միևնույն արտահայտությամբ, որի արժեքը զրոյից տարբեր է:

Հանրահաշվական կոտորակների հետ գործողություններ կատարելիս միշտ ենթադրվում է, որ գործողությունները կատարվում են որոշման տիրույթում (թույլատրելի արժեքների հետ):  

Եթե տրված է A հանրահաշվական կոտորակը, ապա այն −1-ով բազմապատկելով, ստանում ենք՝ (−1)⋅A=−A

A և −A կոտորակները կոչվում են փոխադարձ հակադիր, եթե դրանց գումարը հավասար է 0-ի, այսինքն՝ 

Ինչպես և հակադիր թվերը, հակադիր հանրահաշվական կոտորակները ևս տարբերվում են միայն նշաններով:

Հաճախ հանրահաշվական կոտորակների հետ գործողություններ կատարելիս, պետք է լինում փոխարինել կոտորակի համարիչը կամ հայտարարը հակադիրով: Սակայն, որպեսզի կոտորակի արժեքը չփոխվի, պետք է հետևել նշանի փոփոխության կանոններին՝

կոտորակի արժեքը չի փոխվի, եթե 

— փոխենք համարիչի և հայտարարի նշանները,

— փոխենք համարիչի և ամբողջ կոտորակի նշանները,  

— փոխենք հայտարարի և ամբողջ կոտորակի նշանները:

Եթե A-ով և B-ով նշանակենք հանրահաշվական կոտորակի համարիչն ու հայտարարը, ապա նշանի փոփոխման կանոնը կարելի է գրել հետևյալ կերպ՝  

Կանոնը ուժի մեջ է միայն այն դեպքում, երբ 

Այս հավասարությունները կարելի է ստուգել ցանկացած արժեքի համար հանրահաշվական կոտորակների որոշման տիրույթից:

Հանրահաշվական կոտորակը կրճատելու համար պետք է կոտորակի համարիչը և հայտարարը վերլուծել արտադրիչների: Եթե պարզվի, որ համարիչն ու հայտարարն ունեն ընդհանուր արտադրիչներ, ապա դրանք կարելի է կրճատել:

Արտադրիչների վերլուծման օրինակներ՝

— ընդհանուր արտադրիչի դուրս բերումը փակագծերից,

— կրճատ բազմապատկման բանաձևերի օգտագործումը,

— խմբավորման եղանակ:

Առաջադրանքներ։

1․ Գտնել  c−15c հանրահաշվական կոտորակի արժեքը, եթե c=16

2․ Հետևյալ կոտորակներից ո՞րն է հավասար 3/(x−15)-ի: Ընտրել պատասխանի ճիշտ տարբերակը:

• −(x+15)/−3
• −3/−(x−15)
• (x−15)/−3
• 3/(15−x)
• −3/(15−x)

3․ Կրճատել կոտորակը՝

4․ Հետևյալ կոտորակները բերել 20 x²y հայտարարի

5․ A միանդամը կամ բազմանդամը ընտրեք այնպես, որ ստացվի ճիշտ հավասարություն՝

6․ Կրճատել կոտորակները․

1․ Գրել բացասական ցուցիրով աստիճանի տեսքով․

ա)a^-15
բ)b^-10
գ)c^-5
դ)d^-13
ե)e^-4
զ)n^-6
է)k^-7
ը)17^-18
թ)15^-9
ժ)13^-14

2․ Հաշվել կոտորակի արժեքը․

ա)5^-2, 1.25
բ)16^-1, 1/16
գ)7^-2,1.49
դ)3^-4,1.81
ե)1^-36, 1

3․ Ներկայացնել միանդամի տեսքով․

ա)a⁴b²
բ)c³d¹²
գ)e²⁷k^-45
դ)-m^-30n¹⁰
ե)4k⁶p⁶
զ)-3x^-12y⁴
է)1/3a^-10z⁶
ը)1/2b⁹y^-12

4․ Գրել ամբողջ ցուցիչով աստիճանի տեսքով․

ա) 2⁷
բ) 5⁷
գ) 4⁶
դ) 7⁸
ե) 3¹⁵
զ) 6¹³
է) 11⁶
թ) 9¹⁶

5․ Գրեք ամբողջ ցուցիչով աստիճանի տեսքով․

ա)(5/6)²
բ)(4/25)³
գ)(25/49)⁴
դ) (m/a)¹²
ե) (m/a)⁸
զ) (n/a)¹²

6․ Համեմատել․

ա) 3⁴ > 4³
բ) 2⁴ = 4²
գ) 10²⁰ > 20¹⁰
դ) 100²⁰⁰ > 200¹⁰⁰
ե) 1999²⁰⁰⁰ > 1998¹⁹⁹⁹

նտանիք», «ազգ» և «մշակույթ» բառերը փոխկապակցված են ու իրենց մեջ կրում են լուրջ սոցիալական, պատմական և հոգեբանական նշանակություններ:

1. Ընտանիք – Ընտանիքը հասարակության հիմնական միավորներից մեկն է, որը մարդուն տալիս է պաշտպանություն, սեր, կրթություն ու սոցիալական կազմակերպվածություն։ Ընտանիքը ձևավորում է մեր սկզբնական արժեքներն ու համոզմունքները, հոգևոր և էթիկական համակարգը։

2. Ազգ – Ազգը միավորում է մարդկանց, ովքեր ունեն ընդհանուր լեզու, մշակույթ, պատմություն ու ինքնության զգացում։ Ազգը կազմում է ավելի լայն սոցիալական միավոր, որտեղ մի քանի ընտանիքներ կարող են դառնալ տարատեսակ մշակութային ու քաղաքական կապերով կապված միավոր։

3. Մշակույթ – Մշակույթը այն սովորույթների, արժեքների, հավատալիքների և գործողությունների համակարգն է, որն արտահայտվում է լեզվով, արվեստով, ավանդույթներով, գիտությամբ, կրոնով և այլ ոլորտներում։ Մշակույթը նաև փոխանցվում է սերունդից սերունդ, և այն անընդհատ զարգանում է։

Այս երեք հասկացությունները միաժամանակ կապված են, քանի որ ընտանիքը ձևավորում է մշակույթը, իսկ ազգը ու մշակույթը փոխազդում են, որպեսզի ապահովեն ընդհանուր ինքնություն ու միասնականություն։