10 հետաքրքիր փաստեր Ֆրանսիայի մասին 

1. Սովորաբար եվրոպացիների մեծ մասի համար, մասնավորապես` ֆրանսիացիների, «OK» ժեստը համարվում է վիրավորանք և նվաստացում, այսինքն մարդը ոչնչություն է` զրո:

2.  Ֆրանսիան համարվում է հեծանվի և բալետի հայրենիքը։

3.  Օրենքի համաձայն` ֆրանսիացիները տարեկան ամենաքիչը ունեն հինգ արձակուրդային շաբաթ։

4.  Երեք շուշանները, որոնք պատկերված են Ֆրանսիայի զինանշանին, խորհրդանշում են կարեկցանք, արդարություն և ողորմածություն:

5.  Ամեն տարի Ֆրանսիան հյուրընկալում է ավելի քան 67 մլն տուրիստ, դա ավելին է, քան Ֆրանսիայի բնակչությունը:

6. Ֆրանսիայում թեյավճարը արդեն իսկ ընդգրկված է լինում հաշվի մեջ և կազմում է ընդհանուր հաշվի 15 %-ը:

7.  Ֆրանսիացիները ֆրանսիական համբույրը անվանում են անգլիական համբույր:

8.  Ֆրանսիական որոշ բուրժուական ընտանիքներում մինչև հիմա երեխաները ծնողներին դիմում են «Դուք»-ով:

9.  Փարիզի «Նոր կամուրջը» իրականում ամենահին կամուրջն է բոլոր քաղաքային կամուրջների մեջ:

10. Երեք հարյուր ճանաչված մշակութային գործիչներ բողոքի նամակ են գրել ընդդեմ Էյֆելյան աշտարակի` նշելով, որ այն աղավաղում է Փարիզի տեսքը: Նամակը ստորագրողների թվում են եղել Գի դը Մոպասանը, Շառլ Գունոն, Ալեքսանդր Դյումա-որդին, ճարտարապետ Շառլ Գարնիեն:

Թեմա՝ Բազմանկյուն, ուռուցիկ բազմանկյուն

Բազմանկյուն կոչվում է պարզ փակ բեկյալից և նրանով սահմանափակված տիրույթից բաղկացած պատկերը:

Բեկյալի հանգույցները կոչվում են բազմանկյան գագաթներ, իսկ օղերը՝ կողմեր:

Բազմանկյան մի կողմին պատկանող երկու գագաթները կոչվում են հարևան գագաթներ: Երկու ոչ հարևան գագաթները (որոնք չեն գտնվում նույն կողմի վրա) միացնող հատվածը կոչվում է բազմանկյան անկյունագիծ:

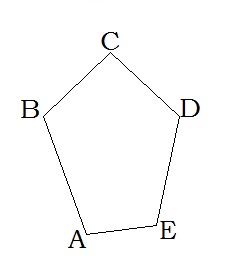
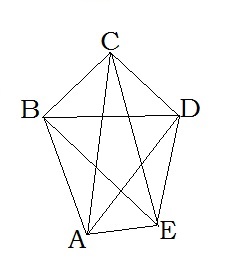
A, B, C, D, E՝ գագաթներ, AB, BC, CD, DE, AE՝ կողմեր, AC, AD, BE, BD, CE՝ անկյունագծեր: 

Բոլոր կողմերի երկարությունների գումարը կոչվում է բազմանկյան պարագիծ: Յուրաքանչյուր քազմանկյուն հարթությունը բաժանում է երկու մասի, որոնցից մեկը կոչվում է բազմանկյան ներքին տիրույթ, իսկ երկրորդը՝ արտաքին տիրույթ

Ուռուցիկ n-անկյան անկյունների գումարը:

Ընդհանուր դեպքում, բազմանկյունը կարելի անվանել n-անկյուն, եթե այն ունի n հատ կողմ, n հատ անկյուն և n հատ գագաթ:

Բազմանկյունը կոչվում է ուռուցիկ, եթե այն ընկած է իր ցանկացած երկու հարևան գագաթներով անցնող մի ուղղի կողմում։

Նկարում պատկերված F₁ բազմանկյունը ուռուցիկ է, իսկ F₂բազմանկյունը ուռուցիկ չէ:

Ուռուցիկ n-անկյան անկյունների գումարը հավասար է 180°⋅(n−2)-ի:

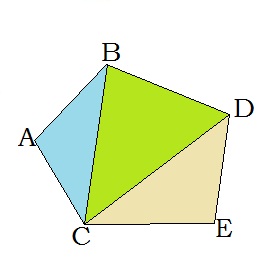
Ցանկացած բազմանկյուն կարելի է բաժանել եռանկյունների: Այդպես է արված վերևի նկարում: Եռանկյունների թիվը  2 -ով քիչ է բազմանկյան կողմերի թվից: Եռանկյունների կողմերը բազմանկյան կողմեր և անկյունագծեր են:

Ցանկացած եռանկյան ներքին անկյունների գումարը 180° է: Հետևաբար, ուռուցիկ n-անկյան անկյունների գումարը 180°⋅(n−2) է:

Հարցեր և առաջադրանքներ։

1. Ո՞ր բազմանկյուն է կոչվում ուռուցիկ։

Բազմանկյունը կոչվում է ուռուցիկ, եթե այն ընկած է իր ցանկացած երկու հարևան գագաթներով անցնող մի ուղղի կողմում։

2․ Ի՞նչ բանաձևով են հաշվում բազմանկյան բոլոր անկյունների գումարը։

Ցանկացած եռանկյան ներքին անկյունների գումարը 180° է: Հետևաբար, ուռուցիկ n-անկյան անկյունների գումարը 180°⋅(n−2) է:

3․ Գծագրել ուռուցիկ հնգանկյուն և վեցանկյուն: Բազմանկյուններից յուրաքանչյուրում որևէ գագաթից տարեք բոլոր անկյունագծերը: Տարված անկյունագծերով քանի՞ եռանկյան է տրոհվում բազմանկյուններից յուրաքանչյուրը:

4. GEOGEBRA ծրագրով գծիր որևէ բազմանկյուն։
ա) Ցույց տուր գագաթները, նշիր կարմիրով

բ) Ցույց տուր կողմերը

գ) Ցույց տուր կից կողմերը

դ) Ցույց տուր հարևան գագաթները։

5.GEOGEBRA ծրագրով գծել ուռուցիկ բազմանկյուն, ինչի՞ է հավասար նրա պարագիծը։

6. GEOGEBRA ծրագրով գծել ոչ ուռուցիկ բազմանկյուն, ցույց տուր որ այն ուռուցիկ չէ։

7. GEOGEBRA ծրագրով գծել ուռուցիկ բազմանկյուն, նշիր նրա արտաքին և ներքին տիրույթները։  Ներքին տիրույթը ներկիր սպիտակ, արտաքին տիրույթը՝ կապույտ։

8.GEOGEBRA ծրագրով գծել եռանկյուն։ Ինչքա՞ն է եռանկյան բոլոր անկյունների աստիճանային գումարը։

9. GEOGEBRA ծրագրով գծել քառանկյուն։ Ինչքա՞ն է քառանկյան բոլոր անկյունների աստիճանային  գումարը։

(4-2)x180=360 աստիճան

10. GEOGEBRA ծրագրով գծել հնգանկյուն։ Ինչքա՞ն է հնգանկյան  բոլոր անկյունների աստիճանային  գումարը։

11. GEOGEBRA ծրագրով գծել վեցանկյուն։ Ինչքա՞ն է վեցանկյան  բոլոր անկյունների աստիճանային  գումարը։

(6-2)x180=720

12․ Գտնել ուռուցիկ հնգանկյան անկյունները, եթե դրանք համեմատական են 2, 3, 4, 5, 6 թվերին:

Ուռուցիկ հնգանկյան անկյունները՝ համեմատական 2:3:4:5:6, կլինեն՝

1. 54°
2. 81°
3. 108°
4. 135°
5. 162°

Անկյունների գումարը՝ 540°։

1․
( ax + 2y = 16 ) հավասարումում տեղադրենք ( (x, y) = (-2, 4) ) թվազույգը՝
( a(-2) + 2(4) = 16 ),
( -2a + 8 = 16 ),
( -2a = 8 ),
( a = -4 ):

2․ Տրված հավասարումներից ( y )-ն արտահայտենք ( x )-ով՝

ա) ( 2x + y = 6 )
( y = 6 — 2x )

բ) ( 3x + y = 7 )
( y = 7 — 3x )

գ) ( x + y — 8 = 12 )
( y = 12 — x + 8 ),
( y = 20 — x )

դ) ( y + 2 = 6x )
( y = 6x — 2 )

ե) ( 3x + 2y = 9 )
( 2y = 9 — 3x ),
( y = \frac{9 — 3x}{2} ),
( y = \frac{9}{2} — \frac{3}{2}x )

զ) ( -4x + 2y = 13 )
( 2y = 4x + 13 ),
( y = 2x + \frac{13}{2} )

3․ Տրված հավասարումներից ( x )-ը արտահայտենք ( y )-ով՝

ա) ( x — y + 5 = 0 )
( x = y — 5 )

բ) ( 2x — 3y + 9 = 0 )
( 2x = 3y — 9 ),
( x = \frac{3y — 9}{2} ),
( x = \frac{3}{2}y — \frac{9}{2} )

գ) ( 15x + y — 8 = 0 )
( 15x = 8 — y ),
( x = \frac{8 — y}{15} )

դ) ( x + 3y — 15 = 0 )
( x = 15 — 3y )

ե) ( 7x + y = 6 )
( 7x = 6 — y ),
( x = \frac{6 — y}{7} )

զ) ( -4x + y = -19 )
( -4x = -y — 19 ),
( x = \frac{y + 19}{4} )

Թեմա՝ Երկու անհայտով առաջին աստիճանի հավասարումներ։

ax+by+c=0                                            (1)

տեսքի հավասարումը, որտեղ a, b, c-ն տված թվեր են, ընդ որում a և b թվերից գոնե մեկը տարբեր է զրոյից, իսկ x-ը և y-ը անհայտներ են, անվանում են x և y երկու անհայտով առաջին աստիճանի հավասարում:

Այդ անվանումը կապված է նրա հետ, որ (1) հավասարման ձախ մասը x և y-ի նկատմամբ առաջին աստիճանի կատարյալ տեսքի բազմանդամ է:

a և b թվերն անվանում են անհայտի գործակիցներ, a թիվը՝ x-ի գործակից, իսկ b թիվը՝ y-ի գործակից:

ax, by, c  արտահայտություններն անվանում են (1) հավասարման անդամներ: Ընդ որում c թիվն անվանում են ազատ անդամ:

(x0,y0)թվազույգն անավանում են (1) հավասարման լուծում, եթե այդ թվերը բավարարում են (1) հավասարմանը, այսինքն՝ x-իփոխարեն տեղադրելով x0, իսկ y-ի փոխարեն y0`հավասարումը վերածվում է ճիշտ թվային հավասարության՝

                                 ax₀+by₀+c=0:

            ax+by+c=0 , որտեղ b հավասար չէ 0                                 (2)

տեսքի ցանկացած հավասարում ունի անթիվ բազմության լուծումներ, որովհետև x-ի համար կարող ենք վերցնել ցանկացած x₀ արժեք, և հավասարումը լուծելով  y անհայտի նկատմամբ կգտնենք 

                            y₀=(-c-ax₀)/b :

(x₀, y₀) թվազույգը կլինի (2) հավասարմանլուծում:

Քանի որ x₀ թվերը անվերջ շատ են, ապա և (2) հավասարման լուծումները անվերջ շատ կլինեն:

x և yերկու անհայտով տված հավասարումից y-ըարատահայտել x-ով՝ նշանակում է լուծել այդ հավասարումը y-ի նկատմամբ ղ-ի ցանկացած տված արժեքի համար:

Օրինակ

                      2x-5y+2=0                    (3)

հավասարումից y-ը արատահայտենք x-ով և գրենքայդ հավասարման բոլոր լուծումները:

Համարենք x-ը կամայական թիվ է, y-ը անհայտն է և լուծենք(3) հավասարումը:

                                          2x+2=5y

                                          5y=2x+2

                                     y=2/5x+2/5                        (4)

Այսպիսով, (3) հավասարման բոլոր լուծումները կլինեն (x;2/5x+2/5) տեսքի, որտեղ x-ը ցանկացած թիվ է:

Դատելով նման կերպ՝ կստանանք, որ 

ax+by+c=0, որտեղ a0տեսքի հավասարումները ունեն անվերջ թվով լուծումներ: Բոլոր այդ լուծումները գրվում են

(-c-by)/a; y) տեսքով, որտեղ y-ը ցանկացած թիվ է:

Առաջադրանքներ

1․
ա) Երկու անհայտով առաջին աստիճանի հավասարում է այն հավասարումը, որը կարող է ունենալ երկու անհայտ՝ x և y, և այդ անհայտների աստիճանները 1 են: Առաջին աստիճանի հավասարումը գծային է, այսինքն՝ գրաֆիկը ուղղի է: Օրինակ՝ 2x + 3y = 5:

բ) ( ax + by + c = 0 ) հավասարման լուծում է այնպիսի ( (x_0, y_0) ) թվազույգը, որի դեպքում x-ի և y-ի արժեքները տեղադրելով հավասարման մեջ՝ ստանում ենք ճիշտ հավասարում: Այստեղ ( a ) և ( b ) գործակիցներից գոնե մեկը պետք է զրոյի չհավասարվի, որպեսզի հավասարումը գծային լինի:

2․ ( x — y + 1 = 0 ) հավասարումը ունի անվերջ լուծումներ, քանի որ սա երկու անհայտով առաջին աստիճանի հավասարում է, և այդպիսի հավասարումները, սովորաբար, անվերջ լուծումներ ունեն:

3․
ա) ( 5x + 4y — 2 = 0 )

բ) ( -3y + 4 = 0 )

գ) ( 2y — 1 = 0 )

դ) ( -5x — y = 0 )

4․ ( x − 2y + 5 = 0 ) հավասարման գործակիցներն են՝ ( a = 1 ), ( b = -2 ), ( c = 5 ):

5․
Տեղադրենք տրված թվազույգերը ( 3x + 2y — 1 = 0 ) հավասարման մեջ.

ա) ( (1; -1) ):
( 3(1) + 2(-1) — 1 = 3 — 2 — 1 = 0 ), այսինքն՝ (1; -1) լուծում է:

բ) ( (5; -7) ):
( 3(5) + 2(-7) — 1 = 15 — 14 — 1 = 0 ), այսինքն՝ (5; -7) լուծում է:

գ) ( (-3; 5) ):
( 3(-3) + 2(5) — 1 = -9 + 10 — 1 = 0 ), այսինքն՝ (-3; 5) լուծում է:

6․ ( 8x + 4y — 8 = 0 ) հավասարումում ( x = 0 ) դեպքում՝
( 8(0) + 4y — 8 = 0 ),
( 4y — 8 = 0 ),
( 4y = 8 ),
( y = 2 ):

7․ ( 13x + 5y = 26 ) հավասարումում ( y = 0 ) դեպքում՝
( 13x + 5(0) = 26 ),
( 13x = 26 ),
( x = 2 ):

8․ ( 3x — 7y + 22 = 0 ) հավասարումից արտահայտենք ( x )-ը՝
( 3x = 7y — 22 ),
( x = \frac{7y — 22}{3} ):

9․ ( ax + 8y = 20 ) հավասարումում տեղադրենք ( (x, y) = (-4, -4) )՝
( a(-4) + 8(-4) = 20 ),
( -4a — 32 = 20 ),
( -4a = 52 ),
( a = -13 ):

10․ ( x + 2y — 24 = 0 ) հավասարումից գտնենք այնպիսի թվազույգ, որի առաջին թիվը 2 անգամ մեծ է երկրորդից, այսինքն՝ ( x = 2y ): Տեղադրենք հավասարման մեջ՝
( 2y + 2y — 24 = 0 ),
( 4y — 24 = 0 ),
( 4y = 24 ),
( y = 6 ),
( x = 2(6) = 12 ):

Ուրեմն ( (12; 6) ) թվազույգը հավասարման լուծում է:

Ծնված 1850 թվականի հունվարի 15-ին, Մոսկվայում (Ռուսաստան)՝ նա առաջին ականավոր ռուս կին մաթեմատիկոսն էր: Նա հակառակվեց իր ծնողներին բարձրագույն կրթություն ստանալու նպատակով: Հայտնի են նրա հետևյալ աշխատանքները.
Նրա դիֆերենցիալ հավասարումների հետազոտությունները  հայտնի են որպես Կովալևսկայայի գագաթնակետ:
Նա աշխատել է  Կոշի-Կովալևսկայայի թեորեմի վրա՝ մի թեորեմ, որ օգնում է հասկանալ դիֆերենցիալ հավասարումները:
13 տարեկանում Սոֆյան ցուցաբերում է արտասովոր ընդունակություն և ոգևորություն  հանրահաշվի և երկրաչափության բնագավառում:

Բայց նրա հայրը կարծում էր, որ հասարակության մեջ չկա ոչ անհրաժեշտություն և ոչ էլ տեղ կրթված կանանց համար: Ուստի նա արգելում է մաթեմատիկայի հետագա ուսումնառությունը: Գաղտնի կերպով Սոֆյան հանրահաշվի գիրք է վերցնում իր ուսուցիչներից մեկից և շարունակում սովորել ՛՛վերմակի տակ՛՛, գիշերը:  
Չնայած մաթեմատիկայի իր ակհայտ տաղանդին՝ նա չկարողացավ ավարտել իր ուսումն Ռուսաստանում: 19-րդ դարում Ռուսաստանի համալսարանները  փակ էին կանանց համար: Մի քանի աղջիկներ էին միայն հասցրել սովորել Շվեյցարիայում և Գերմանիայում, բայց այնուամենայնիվ, Սոֆյան հուսահատորեն փորձեր էր կատարում շարունակել կարիերան որպես բժիշկ կամ քիմիկոս, իսկ նրա հայրը թույլ չէր տալիս լքել հայրական տունը համալսարանում սովորելու համար: Կանայք Ռուսաստանում չէին կարող իրենց  ընտանիքից հեռու ապրել առանց իրենց հայրերի կամ ամուսիների գրավոր թույլտվության: Սոֆյան ստիպված էր ամուսնանալ, որ կարողանա արտասահման գնալ՝ բարձրագույն կրթություն ստանալու: Համապատասխանաբար, նա “ձևական ամուսնություն” է կնքում Վլադիմիր Կովալևսկի հետ՝ երիտասարդ հնեաբանի , ով հետագայում պետք է հայտնի դառնար Չարլզ Դարվինի հետ իր հայտնի համագործակցության համար:
1869-ին Կովալևսկայան սկսեց հաճախել Հեյդելբերգի համալսարան, որտեղ դասախոսների թույլատվությունից անմիջապես հետո  սկսեց  մասնակցել դասընթացներին ազատ ունկնդրի կարգավիճակով:
Հեյդերբերգի համալսարանում երկու տարի մաթեմատիկական գիտություններ սովորելուց հետո նա տեղափոխվեց Բեռլին, որտեղ ստիպված էր մասնավոր դասեր վերցնել Կառլ Վեյերշտրասից, քանի որ համալսարանը նրան նույնիսկ չէր թողնելու ազատ ունկնդրի կարգավիճակով հաճախել: Եթե Հեիդելբերգը դժվար էր կանանց համար, ապա Բեռլինն անհնար էր: Այնպես ստացվեց, որ այդ իրավիճակն  օգտակար եղավ նրա համար, քանի որ հաջորդ չորս տարիներին Վեյերշտրասը նրան մասնավոր դասավանդեց:  Առանց բացառության, կանանց նույնիսկ ոչ պաշտոնական կամ պատահական ներկայությունն արգելված էր դասախոսություններին:
1874 թվականին Կովալևսկայային դոկտորի աստիճան է շնորհել Գեթթինգենի համալսարանը: Չնայած այս աստիճանին և Վեյերշտրասի կողմից տրված երաշխավորագրերին՝ Կովալևսկայան անկարող էր ձեռք բերել պաշտոն կրթության ոլորտում: Դա ուներ մի քանի պատճառներ, բայց նրա սեռը գլխավոր անգելքն էր: Մերժումները տևեցին վեց տարի, որի ընթացքում նա ոչ հետազոտություն նախաձեռնեց, ոչ էլ պատասխանեց Վեյեռստրասի նամակներին:   
Վաղ 1880-ականներին Սոֆյան և նրա ամուսին Վլադիմիրը ֆինանսական խնդիրներ ունեցան: Սոֆյան ցանկացավ դասախոս աշխատել համալսարանում, սակայն նրան չթույլատրվեց, քանի որ նա կին էր, չնայած որ մաթեմատիկայից նույն գիտելիքներն ուներ, ինչ տղամարդիկ: Սոֆյան նույնիսկ առաջարկել էր անվճար դասեր տրամադրել, բայց միևնույն է նրան այդ հնարավորությունը չտվեցին:

Թեման․Արքիմեդի օրենքը։Մարմինների լողալու պայմանները։Նավերի լողալը։Օդագնացություն։

Լաբորատոր աշխատանք․<<Հեղուկի մեջ ընկղմված մարմինն արտամղող ուժի որոշումը>>

Քննարկվող հարցեր․

1․Ո՞րն է հեղուկում արքիմեդյան ուժի առաջացման պատճառը

Արքիմեդյան ուժը հեղուկի խտությունից է. որքան մեծ է հեղուկի խտությունը, այնքան մեծ է արքիմեդյան ուժը: 

2․Ի՞նչ մեծություններից է կախված արքիմեդյան ուժը

Հանգստի վիճակում գտնվող հեղուկի կամ գազի մեջ խորասուզված ցանկացած մարմնի վրա այդ հեղուկի կամ գազի կողմից ազդում է դուրս հրող ուժ, որը հավասար է հեղուկի կամ գազի խտության, ազատ անկման արագացման և հեղուկի կամ գազի մեջ մարմնի խորասուզված մասի ծավալի արտադրյալին։

3․Ձևակերպել Արքիմեդի օրենքը

Հեղուկի կամ գազի մեջ ընկղմված մարմնի վրա ազդում է դուրս մղող մի ուժ, որն ուղղված է ուղղաձիգ դեպի վեր, հավասար է մարմնի արտամղած հեղուկի կամ գազի կշռին և կիրառված է դուրս մղվող մարմնի ծանրության կենտրոնին։ Այդ ուժի մեծությունը որոշվում է մարմնի վրա գործադրված ճնշման ուժերի տարբերությամբ։ Եթե դուրս մղող ուժը փոքր է մարմնի կշռից, ապա մարմինը սուզվում է, իսկ եթե հավասար է՝ լողում է հեղուկում։

4․Ո՞ր դեպքում է մարմինը՝ա․խորասուզվում հեղուկում,բ․լողում նրա ներսում․գ․լողում նրա մակերևույթին։

ա․խորասուզվում հեղուկում,

Եթե մարմնի խտությունը մեծ է հեղուկի խտությունից, մարմինը հեղուկում խորասուզվում է։

բ․լողում նրա ներսում․

Եթե մարմնի խտությունը հավասար է հեղուկի խտությանը, մարմինը լողում է հեղուկի ներսում։

գ․լողում նրա մակերևույթին։

Եթե մարմնի խտությունը փոքր է հեղուկի խտությունից, մարմինը լողում է նրա մակերևույթին:

Սովորել Է.Ղազարյանի դասագրքից(7-րդ դասարան )էջ 151-ից մինչև էջ 163-ը:Պատրաստել նյութ և«Կենդանիների և մարդու լողալը՝էջ158»թեմայի էջ 150-ի թեմայովվերաբերյալ