Այս համարում ներառված են.

• Մաթեմատիկական խաղ. «Սուպեր Մարիո»
• Մաթեմատիկական խաչբառ՝ նվիրված Մխիթար Սեբաստացուն
• Մրգային խնդիր
• Հավասարակողմ եռանկյան տրոհումը հինգ հավասար մասերի. ընթերցողի արձագանքը
• Պարզ թվեր և քառակուսիներ. ընթերցողի արձագանքը
• Գիտե՞ս, որ…
• Երկրաչափության տեսակները
• Հին մաթեմատիկական խնդիրներ Անանիա Շիրակացուց

Մաթեմատիկական խաղ.  «Սուպեր Մարիո»

Արևելյան դպրոցի մաթեմատիկայի ընտրությամբ խմբի  4-5-րդ դասարանցիները ներկայացնում են «Սուպեր Մարիո» մաթեմատիկական խաղը: Խաղի անունը որոշել են սովորողները՝ խաղի քայլերը  նմանեցնելով   համակարգչային խաղ «Սուպեր Մարիոյին»:

Խաղի կանոններն են.
Երկու սովորող դասասենյակում կանգնում են իրար կողք այնպես, որ կարողանան քայլերով ետ ու առաջ անել: Խաղավարը հարցերը ընտրում է այնպես, որ պատասխանները լինեն 1-10 (որպեսզի դասասենյակում տեղավորվեն) թվերը, եթե պատասխանը զույգ թիվ է, այդքան քայլ սովորողները գալիս են առաջ, եթե պատասխանը կենտ է, այդքան քայլ գնում են ետ: Կարելի է նաև փոխել խաղի կանոնները,  զույգ պատասխանի դեպքում՝ ետ գնալ, իսկ կենտ պատասխանի դեպքում՝  այդքան քայլ առաջ գալ: Ընդ որում սովորողները պատասխանները բարձրաձայն չեն ասում, միայն քայլում են: Պարտվում է նա, ով իր քայլը սխալ է կատարում: Երբ սովորողները սկսեն լավ հասկանալ  խաղը, հարցերը կարելի է բարդացնել, օրինակ՝ հաշվել մի քանի գործողությամբ արտահայտության արժեքները: Խաղն ավելի հարմար է խաղալ բակում՝ ազատ և մեծ տարածքում:
Սովորողների  խաղը տե՛ս տեսանյութում:

https://youtube.com/watch?v=ADg3vmpiBbo%3Ffeature%3Doembed

Մաթեմատիկական խաչբառ` նվիրված Մխիթար Սեբաստացուն

Արևմտյան դպրոցի դասավանդող Գրետա Բակունցը  և ընկերները ներկայացնում են մաթեմատիկական խաչբառ՝  նվիրված Մխիթար Սեբաստացուն:

Հարցերը տե՛ս այստեղ:

Մրգային խնդիր

Հյուսիսային դպրոցի երրորդ դասարանի սովորող Կարինե Երիցյանն առաջարկում է մրգային խնդիր և ներկայացնում է  լուծման իր տարբերակը, տե՛ս տեսանյութը:

https://youtube.com/watch?v=HTmAnDHS-Us%3Ffeature%3Doembed

Խորհրդատու՝ Կարին Խառատյան, Հյուսիսային դպրոց:

Հավասարակողմ եռանկյան տրոհումը հինգ հավասար մասերի. ընթերցողի արձագանքը

Հավասարակողմ եռանկյան տրոհումը հինգ հավասար մասերի  նյութի առաջին մասը հրապարակված է «Մաթեմատիկա» ամսագրի  19-րդ համարում: Ընթերցողը հավանաբար կզարմանա, որ այստեղ, որպես մաս, ընդունվում է բարդ կառուցվածք ունեցող չկապակցված պատկերը։ Նախ, մասերի հատկությունների վրա որևէ սահմանափակում չի դրվում։ Երկրորդը, որպես ցուցադրություն, որ այստեղ ոչ մի սարսափելի բան չկա, բերենք օրինակ կյանքից։ Կալինինգրադի մարզը ցամաքային կապ չունի Ռուսաստանի մնացած մասի հետ, բայց դա չի խանգարում, որ նա համարվի Ռուսաստանի մաս։

Սակայն, հարցը, թե կարելի է կանոնավոր եռանկյունը տրովել հինգ հավասար կապակցված մասերի, լրիվ օրինաչափ է։ Բայց նա սպասում է իր պատասխանողին։ Այստեղ էլի մի բաց հարց կա․ ո՞ր N-երի դեպքում է հնարավոր կանոնավոր եռանկյունը բաժանել N հավասար մասերի։ Օրինակ՝ հավասարակողմ եռանկյունը 3, 4, 6 հավասար մասերի տրոհելը հեշտ է (փորձեք)։ Տեսանք, որ 5 մասի բաժանելն էլ արդեն արված է։ Այդպիսի N-երի արժեքները թվարկելու հարցը առայժմ բաց է։ Այսպիսի բարդ կառուցվածք ունեցող մասերի հավասարությունը պետք է հետևյալ կերպ հասկանալ։ Վերցնենք թափանցիկ թղթի թերթ և նրա վրա արտապատկերենք մասերից մեկը, տե՛ս  պատկերը։ Շարժելով և պտտեցնելով թուղթը, պետք ձգտենք, որ այս պատկերը համընկնի մյուս մասերից յուրաքանչյուրի հետ։ Բարեբախտաբար, այս դեպքում հնարավոր է։

Աղբյուրը տե՛ս այստեղ, էջ 8:

Նյութը թարգմանեց Մանկավարժության լաբորատորիայի ղեկավարը՝  Հակոբյան Գևորգը:

«Պարզ թվեր և քառակուսիներ». ընթերցողի  արձագանքը

Ավագ դպրոցի 9-րդ դասարանի սովորող  Գոհար Պետրոսյանը և  նրա ընտանիքն արձագանքել են «Մաթեմատիկա» ամսագրի երրորդ համարին՝  լուծելով Մանկավարժության լաբորատորայի ղեկավարի՝  Հակոբյան Գևորգի առաջարկած «Պարզ թվեր և քառակուսիներ» մաթեմատիկական խաչբառը:

                         Հորիզոնական

a)ամենափոքր պարզ երկնիշ թվի քառակուսին.
11×11=121:
c)քառակուսի, որի վերջին թվանշանը հավասար է հիմքի թվանշանների գումարին  24×24=576, հիմքի թվանշաններն են.
2+4=6
d)քառակուսի, որի թվանշանների գումարը հավասար է հիմքի թվանշանների գումարին.
19×19=361
9+1=10
3+6+1=10
f)եռանիշ ամենամեծ թիվը, որը լրիվ քառակուսի է.

31×31=961
h)պարզ թիվ, որի առաջին երկու թվանշանների տեղերը փոխելով առաջացած թիվը նույնպես պարզ է.
491և  941 թվերը պարզ են
j) պարզ թիվ, որը ստացվում է հորիզոնական d թվի թվանշանների տեղերը փոխելով.
163, 361:
l) ուղղաձիգ գրված q թվի քառակուսին.
241×241= 58081
m) պարզ թիվ, որի երկրորդ թվանշանը 8 է:
181
o)պարզ թիվ, որը առաջին և վերջին թվանշանները նույնն են  և 70-ով մեծ է k ուղղաձիգում գրված թվից.
383=313+70
q)պարզ թիվ, որի առաջին թվանշանը հավասար է մյուսների գումարին.
211, 2=1+1
s) քառակուսի, որ վերջին երկու թվանշանները նույնն են.
12×12=144
t)պարզ թիվ, որը 100-ով մեծ է i ուղղաձիգում գրված թվից:
151+100=251
u)պարզ թիվ, որի առաջին երկու թվանշանների գումարը հավասար է երրորդին:
167, 1+6=7

                                 Ուղղաձիգ

a)քառակուսի, որը գրվում է նույն թվանշաններով, ինչ f հորիզոնականի թիվը.
13×13=169
b)պարզ թիվ, որի առաջին և վերջին թվանշանները նույնն են.
131
c)քառակուսի, որի առաջին թվանշանը հավասար է հիմքի թվանշանների գումարին.
23×23=529
e)քառակուսի, որը գրվում է նույն թվանշաններով, ինչ a ուղղաձիգում գրված թիվը.
169, 196
g) t հորիզոնականում գրված թվի քառակուսին.
251×251=63001
h) քառակուսի, որի առաջին երկու թվանշանները նույնն են.
21×21=441
i)պարզ թիվ, որը սկսվում և վերջանում է 1-ով.
151
j) պարզ թիվ, որը ստացվում է b ուղղաձիգում գրված թվի երկրորդ և երրորդ թվանշանների տեղերը փոխելով.
131, 113
k) պարզ թիվ, որի երկրորդ թվանշանը 1 է.
313
n) քառակուսի, որի առաջին թվանշանը երկու անգամ մեծ է երկրորդից.
29×29=841, 4×2=8
p)պարզ թիվ, որի առաջին երկու թվանշանները նույնն են.
881
q)պարզ թիվ, որը 10-ով փոքր է t հորիզոնականում գրված թվից.
251-10=241
r) պարզ թիվ, որը 6-ով մեծ է a հորիզոնականում գրված թվից:.
121+6=127
Աղբյուրը տե՛ս այստեղ:

Խորհրդատու՝ Միջին դպրոցի դասավանդող Լիանա Հակոբյան:

Գիտե՞ս, որ…

Գիտես, որ բոլոր այն եռանիշ թվերը, որոնք գրառվում են  միևնույն թվանշաններով, բաժանվում են 37-ի:

111: (1+1+1)=37

222: (2+2+2)=37

555: (5+5+5)=37

666: (6+6+6)=37

777: (7+7+7)=37

888: (8+8+8)=37

999: (9+9+9)=37

Նյութը ներկայացրեց  Միջին դպրոցի դասավանդողը՝ Զարինե Փանյանը:

Երկրաչափության տեսակները

Ավելի քան 2000 տարի առաջ հույն մաթեմատիկոս Էվկլիդեսը սկսել է մարդկանց բացատրել, որ ցանկացած մաթեմատիկական դատողություն, վարկած պետք է ապացուցվի։ Ինչքան էլ, որ մի պնդում կարող է ճշմարիտ լինել, կա որոշակի հավանականություն, որ այդ պնդումը կարող է նաև լինել կեղծ, այնպես որ համոզված լինելու համար պետք է ապացույց ունենալ։

Հիմա, եթե մենք սկսում ենք ապացույցներ տալ, պետք է ինչ-որ տեղից սկսենք։ Չենք կարող անընդհատ ապացուցել, ապացուցել և այդպես անվերջ տարբեր բաներ ապացուցել՝ անընդհատ գալով պարզ մաթեմատիկայի հիմունքներին։ Էվկլիդեսն էր, որ արեց այդ ապշեցուցիչ քայլը՝ հասկացավ, որ մաթեմատիկան ունի աքսիոմների կարիքը։ Աքսիոմը, կոպիտ ասած, ինչ-որ բանի հիմնավորման համաձայնեցված ելակետն է, որը ապացուցման կարիք չունի։ Օրինակ, մենք կարող ենք համաձայնել, որ ցանկացած երկու կետով անցնում է մեկ ուղիղ, կամ էլ, որ ցանկացած երկու ուղիղ հատում են մեկ կետում։ Արդյունքում, Էվկլիդեսի ասելիքը սա էր․ «Եկեք համաձայնության գանք որոշ հիմնական «փաստերի» շուրջ և համաձայնվենք, որ դրանցից բացի մնացած ամեն ինչը պետք է ապացուցվի»։ Ասելով դա, նա կազմեց այն աքսիոմները, որոնք մենք գիտենք, որպես Էվկլիդեսյան երկրաչափություն, ու այդպիսով նա սկսեց զարգացնել երկրաչափությունը ու այն հասցնել շատ բարձր մակարդակի։ Սա այն երկրաչափությունն է, որը մենք սովորում ենք դպրոցում և օգտագործում ենք կենցաղում, օրինակ՝ երբ տուն ենք նախագծում։

Ամեն ինչ լավ է թվում, բայց ենթադրենք, թե չենք համաձայնվում Էվկլիդեսի աքսիոմների հետ։ Հետո՞ ինչ է լինում։ Նախ և առաջ, մենք չենք կարող անվավեր ճանաչել Էվկլիդեսի փաստարկները, չնայած նրան, որ նա ասում է «եթե համաձայն ենք իմ աքսիոմներին, ապա սա այսպես կլինի, դա էլ այդպես կլինի»։ Մենք չենք կարող կասկածի տակ դնել Էվկլիդեսի աքսիոմները, եթե նույնիսկ մենք մեր աքսիոմներն ենք նախընտրում։ Այնուամենայնիվ, նշանակում է, որ մեկը կարող է գալ և փոփոխությունների ենթարկել Էվկլիդեսի աքսիոմները, ինչից հետո, ենթադրաբար նրանք կհանգեն ուրիշ թեորեմների։ Եկեք փորձենք։

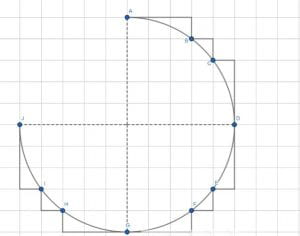
Պատկերացրեք, որ ուզում ենք շրջագայել Երկրագնդի շուրջ և այդպիսով, լինելով մի «նավիգատոր»՝ ուզում ենք չափել հեռավորություններ, անկյուններ և այլ բաներ՝ Երկրի մակերույթի վրա։ Դա նշանակում է, որ մենք պետք է երկրաչափություն անենք գնդի մակերևույթի վրա։ Ակնհայտ է, որ Էվկլիդեսյան երկրաչափությունը չի աշխատի այստեղ։ Ի՞նչ պետք է անենք։ Պետք է փոփոխության ենթարկենք աքսիոմները և (կամ) ստեղծել նոր երկրաչափություն։ Եկեք ստանանք նոր երկրաչափություն։

Գնդի վրա երկու կետերի միջև եղած ամենափոքր հեռավորությունը Մեծ շրջանի (շրջան որն առաջանում է գունդը այնպիսի հարթությամբ հատելիս, որն անցնում է այդ գնդի կենտրոնով) մի աղեղ է։ Երկիր մոլորակի մակերևույթի երկայնության և հասարակածի գծերը Մեծ շրջաններ են։ Մնացած երկայնության գծերը Մեծ շրջաններ չեն, քանի որ դրանց կենտրոնները չեն համապատասխանում Երկիր մոլորակի կենտրոնին։ Այսինքն կարելի է ասել, որ ողջամիտ կլինի ասել, որ Մեծ շրջանները մեր նոր՝ գնդային երկրաչափության ուղիղներն են։ Քանի՞ այդպիսի ուղիղ կա տարված Հյուսիսային և Հարավային բևեռների կետերով։ Այդ թիվն անվերջության պես շատ է։ Էվկլիդեսի աքսիոմներից մեկում ասվում է, որ երկու կետերով հնարավոր է անցկացնել միայն մեկ ուղիղ, սակայն գնդային երկրաչափությունում այս աքսիոմը, ինչպես տեսաք, պետք է փոխել։

Եկեք պատկերացնենք եռանկյուն մի գնդի վրա, որի գագաթները դրված են 1․ Հյուսիսային բևեռի կետում, 2․հասարակածի և Գրինվիչյան միջօրեականի հատման կետում, 3․հասարակածի 90 աստիճան երկայնությամբ կետում։ Այս երեք կետերն իրար միացնող Մեծ շրջանների աղեղները ստեղծում են գնդային երկրաչափության եռանկյուն, որը կազմված է 90 աստիճան ունեցող անկյուններով։ Ստացվում է, որ գնդային երկրաչափությունում ևս մեկ բան կա, որը չի համապատասխանում Էվկլիդեսյան երկրաչափությանը։ Ինչպես տեսանք, կոնկրետ այս եռանկյան անկյունների գումարը ստացվեց 270 աստիճան, այնինչ, ըստ Էվկլիդեսի՝ բոլոր եռանկյունների անկյունների գումարը 180 աստիճան է։ Մաթեմատիկոսները պարզել են, որ գնդային երկրաչափության եռանկյան անկյունների գումարը կարող է լինել 180 աստիճանից մինչև 540 աստիճան։ Այսպես կարելի է անվերջ շարունակել այս փոփոխվող աքսիոմների շարքը։ Օրինակ՝ գնդային երկրաչափությունում ցանկացած երկու Մեծ շրջան(Էվկլիդեսյան երկրաչափության ուղիղները) հատվում են 2 կետերում, իսկ Էվկլիդեսյանում դրանք հատվում են միայն մեկում։

Կարծում եմ, որ մենք հասանք այն կետին, որ պետք է համաձայնվենք, որ կան առնվազն 2 տարբեր երկրաչափություններ՝ ի դեմս Էվկլիդեսյան երկրաչափության և գնդային երկրաչափության։ Այդ երկու երկրաչափություններն իրար չեն հակասում, դրանցից ոչ մեկը ո՛չ ճիշտ է, ո՛չ էլ սխալ։ Դրանք պարզապես շարունակությունն են հազարամյակներ առաջ Էվկլիդեսի սկսածի, պարզապես տարբեր հիմնավորման ելակետերով՝ աքսիոմներով։ Զարմանալին այն է, որ Երկրի վրա անընդհատ շրջագայող մարդուց դարեր պահանջվեցին, որպեսզի նա հասկանար, որ Էվկլիդեսյան երկրաչափությունից բացի կան այլ՝ նույնպես վավեր և ծանրակշիռ երկրաչափություններ։

Եվ ուրեմն, ինչպե՞ս կարող ենք պատասխանել այս հոդվածի վերնագրի հարցին։ Դե, սա ուրիշ և շատ երկար պատմություն է, բայց վերջում ստացվում է, որ իրականում կան շատ-շատ երկրաչափություններ, ամենքը իր առանձնահատկությոններով։ Որոշները հետաքրքիր և օգտակար են (ինչպես օրինակ գնդային երկրաչափությունը կամ Էյնշտեյնի հարաբերականության տեսության կոր տարածությունները), որոշներն էլ պարզապես հետաքրքրասիրություններ են։ Այնուամենայնիվ, շնորհիվ Էվկլիդեսի, որը ցավոք երբեք չհասցրեց պատկերացնել այդպիսի բաներ, մենք գիտենք, որ բոլոր երկրաչափությունները վավեր են և ամենքն իր հատկությունները ունի։ Հետաքրքիր է, թե հիմա մենք որտեղ կլինեինք, եթե հանճարեղ Էվկլիդեսը ի վիճակի լիներ ևս մի զարմանահրաշ քայլ անել աշխարհում 2000 տարի առաջ՝ հասկանալ, որ այլ երկրաչափություններ էլ կան։

Նկարիչ Մ․ Ս․ Էսչերը օգտագործել է տարբեր՝  գնդային, հարթաչափական և հիպերբոլիկ երկրաչափություններ և ստացել հրաշալի նկարներ։

Թարգմանությունը  կատարեց Ավագ դպրոցի 10-րդ դասարանի  սովորող  Արամ Պետրոսյանը:

Նյութի աղբյուրը տե՛ս  այստեղ։
Հոդվածի հեղինակն է Ալան Բերդոնը։
Խորհրդատու՝ Ավագ դպրոցի դասավանդող Հերմինե Անտոնյան:

Հին մաթեմատիկական խնդիրներ Անանիա Շիրակացուց

Միջին դպրոցի դասավանդող Հասմիկ Իսրայելյանը և ընկերները ներկյացանում են Անանիա Շիրակացու՝ «Յաղագս հարցման և լուծման» գրքից մի քանի  խնդիրներ, որոնք  թարգմանել են աշխարհաբար:

Խնդիր 1․ Ես իմ հորից լսել եմ, որ պարսիկների դեմ հայոց պատերազմի ժամանակ Զորաց Կամսարյանը մեծ քաջագործություններ էր գործում․ իբր թե մեկ ամսվա ընթացքում երեք անգամ հարձակվելով պարսկական զորքի վրա՝ առաջին անգամ կոտորեց զորքի կեսը, երկրորդ անգամ՝  քառորդ մասը, երրորդ անգամ՝ տասնմեկերորդը, մնացածները՝ թվով 280 մարդ, փախուստի մատնված, Նախիջևան մտան: Քանի՞ մարդ կար ջարդի սկզբում:

Խնդիր 2. Իմ մերձավոր մարդկանցից մեկը, մեկնելով Բահլ, շահաբեր գնով մարգարիտ ձեռք բերեց։ Տուն վերադառնալիս, հասնելով Գանձակ, նա իր գնած մարգարտի կեսը վաճառեց հատը 50 դրամով։ Գալով Նախիջևան՝ վաճառեց մնացածի  քառորդ մասը հատը 70 դրամով, ապա հասնելով Դվին՝ վաճառեց նաև այդ մարգարտի 1/12 մասը հատը 50 դրամով։ Երբ նա եկավ մեզ մոտ՝ Շիրակ, նրա մոտ մնացել էր ընդամենը 24 հատ մարգարիտ։ Ընդամենը քանի՞ մարգարիտ էր գնել և որքա՞ն դրամ էր ստացել վաճառած մարգարիտներից։

Խնդիր 3. Ես իմ ուսուցչից լսեցի, թե գողերը, մտնելով Մարկիանոսի գանձարանը, գանձի կեսը և մնացածի մեկ քառորդը մասը  գողացան։ Գանձապահները ներս մտնելով գտան 421 կենդինար (1 կենդինարը հավասար է 7200 դահեկանի) և 3600 դահեկան։ Որքա՞ն գանձ կար գանձարանում։

Խնդիր 4. Սպաների աշխատավարձը բաշխվում էր այսպես․ 1/4 մասը՝ պատվազորներին, 1/8-ը` ավագներին, իսկ մնացած 150 կենդինարը՝ մյուս հեծյալներին։ Իմացի՛ր, թե ամբողջ աշխատավարձը որքան էր։

 Խորհրդատու՝ Հասմիկ Իսրայելյան, Միջին դպրոց:

 Համարի պատասխանատուներ.

• Թողարկող, խմբագիր՝  Մարիա Աբրահամյան, Միջին դպրոց,  8-րդ դասարան

Սովորողներ.

• Կարինե Երիցյան. Հյուսիսային դպրոց, 3-րդ դասարան
• 4-5-րդ դասարանների մի խումբ սովորողներ. Արևելյան և Արևմտյան դպրոց
• Գոհար Պետրոսյան. Ավագ դպրոց, 9-րդ դասարան
• Արամ Պետրոսյան. Ավագ դպրոց 10-րդ դասարան

Դասավանդողներ՝

• Կարինե Խառատյան, Հյուսիսային դպրոց
• Գրետա Բակունց, Արևելյան դպրոց
• Զարինե Փանյան, Միջին դպրոց
• Հերմինե Անտոնյան, Ավագ դպրոց
• Հասմիկ Իսրայելյան, Միջին դպրոց
• Լիանա Հակոբյան, Միջին դպրոց
• Գևորգ Հակոբյան, Մանկավարժության լաբորատորիա

Այս համարում ներառված են հետևյալ նյութերը.

1. Ինչպե՞ս վանդակավոր թղթի վրա գծել շրջանագիծ՝ առանց կարկինի օգնության:
2. Ինչպե՞ս են առաջացել երկրաչափական պատկերների անվանումները:
3.Խնդիրների թարգմանություն «Քվանտ » ամսագրից:

1. Ինչպե՞ս վանդակավոր թղթի վրա գծել շրջանագիծ՝ առանց կարկինի օգնության

Երկրաչափության դասն է: Անհրաժեշտ է տետրում գծել շրջանագիծ, բայց ավաղ, կարկին չկա: Իհարկե, կարելի է դուրս գալ իրավիճակից և նկարել շրջանագիծ ձեռքով՝ օգտվելով միայն տետրի վանդակներից: Պետք է միայն հիշել հետևյալ թվերը՝ երեք-մեկ, մեկ-մեկ, մեկ-երեք: Շրջանագիծը սկսեք նկարել սկզբնակակետ համարելով տետրի հորիզոնական և ուղղահայաց գծերի հատման որևէ կետ: Հատման այդ կետը նշանակենք A տառով: Աչքաչափով տանենք կոր գիծ՝ ասելով երեք-մեկ: Սա նշանակում է, որ A կետից պետք է տեղաշարժվել դեպի B կետ, երեք վանդակ շարժվելով աջ և մեկ վանդակ՝ դեպի ներքև: Տես նկարը՝

Այնուհետև B կետից տեղաշարժվենք դեպի C կետ՝ ասելով մեկ-մեկ, սա նշանակում է, B կետից պետք է շարժվել մեկ վանդակ դեպի աջ և մեկ վանդակ՝ դեպի ներքև: Տես նկարը՝

Այժմ, շարունակենք և վերջապես C կետից տանենք կոր գիծ դեպի D կետը: ABCD կոր գիծը կլինի շրջանագծի ¼ մասը: Տես նկարը՝

D կետից գնանք դեպի E, նորից ասելով երեք-մեկ, այս անգամ շարժվելով երեք վանդակ ներքև և մեկ վանդակ՝ դեպի ձախ: Այնուհետև կասենք՝ մեկ-մեկ և մեկ-երեք: Ստացվում է, որ գծագրում ավելացան DEFG կետերը: Տես նկարը՝

Շրջանագծի ½ մասը արդեն գծել ենք: Նույն ձևով կարելի է գծել մյուս քառյակը՝ GHIJ: Տես նկարը՝

Վերջին կետերը՝ JKLA-ն կառուցելով ճիշտ նույն ձևով, կհասնենք սկզբնակետին՝ A կետին և մեր շրջանագիծը պատրաստ է, տես նկարը:

Նյութի աղբյուրը տես այստեղ:

Տեսանյութը ներկայացնում է Աբել Բաբայանը: 

https://youtube.com/watch?v=uz_WsUC9dFM%3Ffeature%3Doembed

2.Ինչպե՞ս են առաջացել երկրաչափական պատկերների անվանումները:

Բոլոր երկրաչափական պատկերների, մարմինների անվանումները ի սկզբանե կոչվել են ինչ- որ առարկաների անուններով, շատ թե քիչ մոտ լինելով տվյալ մարմնի կառուցվածքին։

Բուրգ– Հունարեն բառի πυραμίδα լատիներեն ձևն է, որով հույները անվանել են եգիպտական բուրգերը։ Այս բառը գալիս է հին եգիպտական «Պուրամա» բառից, որով էլ անվանել են այդ բուրգերը։ Ժամանակակից եգիպտացիները բուրգերը կոչում են «Ախրամ», որը նույնպես գալիս է այդ հին եգիպտական բառի արմատից։

Բուրգ բառի բացատրությունն ըստ Հրաչյա Աճառյանի արմատական բառարանի՝

Բուրգ-1.Երկրաչափական մարմին, որն ունի բազմանկյունի նիստ և որի եռանկյունաձև կողերը միանում են մի կետում: 2.Քառակուսի նիստով և հետզհետե նեղանալով բարձրացող քարե մեծ կառույց: 3.Աշտարակ կամ աշտարակաձև կառույց:

Սեղան բառը ծագում է լատինական trapezium բառից, հունարեն բառի τραπέζι լատիներեն ձևն է: Հունարեն տրապեզիում բառը նշանակում է «սեղան» : Հենց այդ արմատից է գալիս մեր բառը՝ «տրապեզա», որը հունարեն նշանակում է սեղան :

Նայենք բառի բացատրությունը ըստ Հրաչյա Աճառյանի արմատական բառարանի՝

Սեղան-1.Ճաշի սեղան: 2. Հացկերույթ: 3. Զոհասեղան:

Շեղանկյուն բառը ծագում է լատիներեն «rombus» բառից, հունարեն բառի διαγώνιος լատիներեն ձևն է: Ռոմբուս բառը նշանակում է երաժշտական գործիք՝ բուբեն։ Մենք սովոր ենք, որ այդ գործիքը պետք է լինի շրջանաձև, բայց առաջ այն ունեցել է քառակուսու կամ շեղանկյան ձև, ինչի մասին են վկայում խաղաքատերի վրայի նկարները:

Կետ-Լատիներեն լեզվից punkt «պունկտ» բառն է, որը նշանակում է ներարկում: Այդ բառի արմատից է ծագում բժշկական պունկցիա՝ ներկարկում բառը:

Գիծ բառը ծագում է լատիներեն linea բառից որը նշանակում է թել:

Ուղիղ բառի բացատրությունն ըստ Հրաչյա Աճառյանի արմատական բառարանի.

Ուղիղ-առանց ծռվելու, թեքվելու մի գծով ձգված ուղղություն:

Նյութի աղբյուրը տե՛ս այստեղ:

3.Խնդիրների թարգմանություն «Քվանտ» ամսագրից:

1.Ընտրեք երեք տարբեր թվանշաններ այնպես, որ քառանիշ թվերի շարքում, այդ թվանշաններով հնարավոր լինի կազմել այնպիսի թիվ, որ բաժանվի՝ 2, 3, 4, 5, 6, 7, 8, 9 և 10-ի:

2.Դահլիճում կան ստախոսներ և ասպետներ: Ստախոսները միշտ ստում են, իսկ ասպետներ խոսում են միայն ճշմարիտ: Յուրաքանչյուրը մատնանշեց դահլիճի ներկաներից որևէ մեկին և ասաց, որ վերջինս ստախոս է: Պարզվեց, որ ներկաներից յուրաքանչյուրին ասել են այդպիսի արտահայտություն: Դահլիճում կարո՞ղ է լինել 101 մարդ:

3. Երեք հեծանվորդներ շարժվելով միևնույն կետից, նույն ողղությամբ սկսեցին իրենց շարժումը օղակաձև ճանապարհով: Դրանցից առաջինը ամբողջ ճանապարհն անցավ 5 րոպեում, երկրորդը ՝ 7 րոպեում, երրորդը ՝ 9 րոպեում: Ամենաքիչը քանի՞ րոպե անց, բոլոր հեծանվորդները կհայտնվեն ճանապարհի միևնույն կետում, եթե բոլորը շարժվում են հաստատուն արագությամբ:

4.Դիտարկենք 8 հարթություն, որոնցից յուրաքանչյուրն անցնում է խորանարդի ճիշտ 3 գագաթներով: Կտրենք խորանարդը բոլոր այդ հարթություններով: Խորանարդի կենտրոնում ի՞նչ պատկեր կստացվի։

Նյութի աղբյուրը տե՛ս այստեղ:

Պատասխանատուներ.

Թողարկող, խմբագիր՝ Մարիա Աբրահամյան, Միջին դպրոց, 7-րդ դասարան

Աշխատանքը թարգմանեցին՝

Անահիտ Վերմիշյան, Միջին դպրոց, 7-րդ դասարան

Մարկ Հովհաննիսյան, Միջին դպրոց, 7-րդ դասարան

Նանե Ժամհարյան, Միջին դպրոց, 7-րդ դասարան

Տեսանյութի, նկարների հեղինակ՝ Աբել Բաբայան, Միջին դպրոց, 7-րդ դասարան

Հետևելով ամսագրում նշված քայլերին, դու էլ փորձիր գծել շրջանագիծ առանց քանոնի օգնության, աշխատանքդ ներկայացրու բլոգում: Թղթի վրա շրջանագիծ գծելու համար ուրիշ ի՞նչ ճանապարհներ գիտես: (բաժակով և կլոր ինչվոր իրով )

Երկրաչափություն

Երկրաչափություն (հին հունարեն՝ γεωμετρία; geo- «երկիր», -metria «չափումներ»), մաթեմատիկայի ճյուղ, որը ուսումնասիրում է մարմինների մակերևույթը, չափերը, միմյանց նկատմամբ դասավորությունը և տարածության հատկությունները։

Երկրաչափությունը մի շարք վաղ մշակույթներում միմյանցից անկախ, ծագեց որպես երկարության, մակերեսի և ծավալի հետ գործելու պրակտիկ եղանակ։ Երկրաչափությունը, արևմուտքում ձևավորված ֆորմալ մաթեմատիկական տարրերը սկսեց օգտագործել դեռևս մ․թ․ա․ 6-րդ դարում^[1]։ Մ․թ․ա․ 3-րդ դարում Էվկլիդեսը իր Տարրեր աշխատությունում երկրաչափությունը դրեց աքսիոմատիկ հիմքերի վրա, որով գործածման ստանդարտներ սահմանեց դարեր ի վեր^[2]։ Երկրաչափությունը Հնդկաստանում ծագեց անկախ, մ․թ․ա․ 3-րդ դարում, ապահովելով երկրաչափական մարմինների միջև գոյություն ունեցող կանոնների նկարագրությունը^[3]։ Մուսուլման գիտնականները վերցնելով հույների գաղափարները միջին դարերում դրանք զարգացրեցին^[4]։ 17-րդ դարի սկզբին Ռենե Դեկարտի և Պիեռ Ֆերմայի կողմից երկրաչափությունը ամուր անալիտիկ հիմքերի վրա դրվեց։ Այդ ժամանակներից ի վեր և մինչ արդի ժամանակները, երկրաչափությունը ընդարձակվել է դեպի ոչ-Էվկլիդեսյան երկրաչափություն և տոպոլոգիական բազմազանություններ, որոնք ընկած են մարդկային փորձի սովորական սահմաններից դուրս^[5]։

Չնայած երկրաչափությունը տարիների ընթացքում զգալիորեն զարգացել է, սակայն կան ընդհանուր հասկացություններ, որոնք քիչ թե շատ հիմնարար են երկրաչափության համար։ Դրանցից են կետերը, ուղիղները, հարթությունները, մակերևույթները, անկյունները և կորերը, ինչպես նաև ավելի ընդլայնված հասկացություններ, ինչպիսիք են բազմազանության, տոպոլոգիայի և մետրիկայի հասկացությունները^[6]։

Երկրաչափությունը կիրառվում է բազմաթիվ բնագավառներում, ներառյալ արվեստը, ճարտարապետությունը, ֆիզիկան, ինչպես նաև մաթեմատիկայի այլ ճյուղերը։